The Life of Ryan

Mandelbox Explorer

Ray Marching Demonstration

Play demo controls (auto move)

Controls

Key	Description
W,A,S,D,C,Space	Move camera position.
Mouse-Click&Drag	Change the pitch and yaw of the camera.
Shift	Hold to reduce manual movement speed.
F	Enable fullscreen if not enabled.
P	Toggle playing the demo controls.
R	Restore camera values to their default.

Explanation

This scene is a demonstration of the Mandelbox 3D fractal. The geometry is rendered using a technique called ray marching, wherein each pixel is the result of casting a ray incrementally through space. At each iteration, a signed-distance function is applied to the current position of the ray to determine the closest distance to the fractal. This determines how far the ray will move along its direction, and a collision is determined when the function's return-value is non-positive.

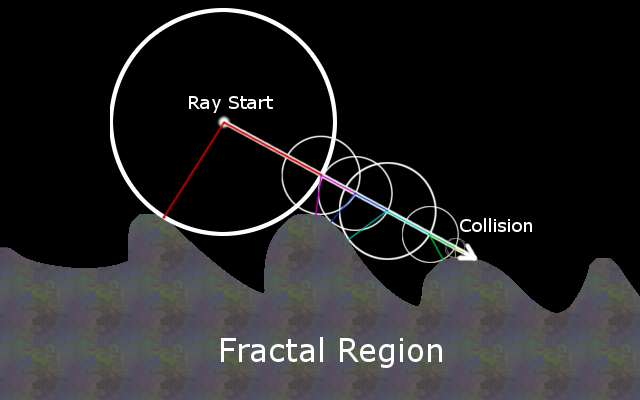
At each iteration of the algorithm, the ray will only move as far as the closest distance to the region.

Mandelbox Signed-Distance Function

function signedDistance(point, mandelboxScale /*scale must be less than -1*/) {
    let DEfactor = 1.0;
    let r2 = 1.0;
    let maxR2 = 12.0;
    let float BVR = sqrt(maxR2);
    for(let i = 0; i < MAX_ITERATIONS; i++) {
        // Apply box-folding where each component is linearly folded in space back to the domain [-1, 1]
        if(point.x > 1.0){point.x = 2.0 - point.x;} else if(point.x < -1.0){point.x = -2.0 - point.x;}
        if(point.y > 1.0){point.y = 2.0 - point.y;} else if(point.y < -1.0){point.y = -2.0 - point.y;}
        if(point.z > 1.0){point.z = 2.0 - point.z;} else if(point.z < -1.0){point.z = -2.0 - point.z;}

        r2 = dot(point, point);

	// Apply spherical-folding 
        if(r2 < 0.25) {
            point *= 4.0;
            DEfactor *= 4.0;
        } else if(r2 < 1.0) {
            point /= r2;
            DEfactor /= r2;
        }

        point = point*mandelboxScale + t;
        DEfactor = DEfactor*abs(mandelboxScale) + 1.0;

        if(r2 < maxR2) break;
    }
    return (length(point)-BVR)/abs(DEfactor);
}